packed memory arrays-rewired

前置知识

(a,b)-tree

(a,b)-tree是一个平衡的(所有的叶子在同一层)搜索树，

• 2≤a≤(b+1)/2,当a==(b+1)/2时 为b-tree
• 根结点最多有b个子结点。
• 除了根节点之外，每个内部节点至少有a个子节点，最多有b个子节点。
• 所有从根到叶的路径都是相同的长度。

(2,3)-tree 是b树 (a,b)-tree相当于b-tree的扩展,b-tree是(a,b)的特例.

https://cs.lmu.edu/~ray/notes/abtrees/

https://en.wikipedia.org/wiki/(a,b)-tree

传统 PMAa

一个数组，其中的元素是按照排序的顺序存储的，交叉元素或间隙。间隙的目的是提供额外的空间，以便在数组的任意位置插入新元素，而不需要移动现有元素的长序列来维持排序顺序。

PMA的实现

搜索数组中的元素可以通过二分搜索利用排序顺序来实现。范围扫描包括在范围的两个端点之间对数组进行顺序迭代。这里，空槽被简单地忽略。要插入新元素，算法首先在数组中搜索它的目标槽。但是，如果该位置已经被另一个元素e占据，则算法首先将e和e的所有相邻元素移向数组中最接近的间隙。最后，要删除数组中的元素，算法只需将其槽标记为空。

在部分数据变得过于稀疏或过于密集时，在本地重新调整数据结构。

1. 定位要插入元素的位置。我们要么事先知道这个，要么执行代价为O(log2N)的二分查找。
2. 如果我们要插入的单元格是空闲的，我们只需添加元素，并将该单元格标记为used。
3. 但是，如果要插入的单元格被使用了，我们计算所需单元格所在的最小块(大小为log N)的上限密度阈值，并检查是否会违反上限密度阈值。如果我们注意到没有超过阈值，我们只需重新平衡所有元素，包括新的元素到那个块中。如果我们违反了较高的密度阈值，我们考虑一个两倍大的块(其中包括我们将插入的单元格)，并检查是否违反了密度阈值。我们不断向上移动，直到找到一个不违反上密度阈值的块。
4. 如果我们找不到这样的块，我们就分配一个两倍大的数组，并整齐地将所有现有的元素复制到新的数组中，元素之间的间隔是恒定的.

APMA

hammering 敲打指的是连续且频繁的插入发生在数组的相同区域。

在hammering发生的段放置更多的gap,但也可能会出现乒乓效应,性能甚至不如传统PMA.

如图所示,最后插入的是14,15,16.apma认为在第一段中插入数据过多,于是在rebalance的过程中在第一段中放置更多的gap,但是实际上的插入序列如果是17,18,19,则性能可能会很差.

Calibrator tree

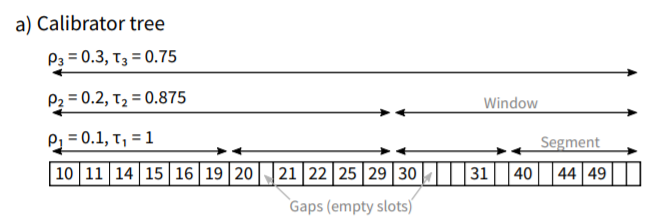
摘要

基于树的索引结构的物理内存布局会随着时间的推移而恶化(比如B-树中的合并与分裂),物理级别上的顺序扫描就会变成非顺序的，因此扫描操作会变慢.Packed Memory Arrays(PMA)通过管理所有数据在一个顺序稀疏阵列来防止顺序扫描变成非顺序的。本文在PMA的基础上提出了一个改进的数据结构:Rewired Memory Array(RMA)。RMA可以达到具有竞争力的更新和点查找性能，同时始终提供优越的扫描性能-接近密集列扫描。

介绍

针对列存存储引擎,本文提出了一种基于PMA的数据结构。列存变得稀疏而不是密集。在存储的元素中有空的间隙，以适应未来可能的更新。因此，可以直接就地执行更新。扫描是顺序的，比(a,b)-tree快. 更新可以在对数复杂度完成，但比不上(a,b)-tree。

有几个因素会阻碍稀疏数组的性能。对于扫描，通过检查数组的每个插槽是否被填满，需要付出大量的CPU 代价。对于更新，数据结构偶尔需要重新平衡，这增加了这些操作的平均成本。此外，在重新平衡期间，数组中的元素可能会被移动，这也会导致PMAs的索引分隔符键的更新.(索引存储每个段的最小key).在存在数据倾斜的情况下，稀疏数组会遇到最坏的情况，并且在更新期间会进行更多的内部重组.

主要贡献

• 通过提出cluster、固定大小的段、静态索引和内存重布线，克服了scan的一些性能问题，同时减少了内部重平衡的延迟。
• 对自适应再平衡进行了改进。自适应再平衡减少了出现更新倾斜时发生的再平衡数量。尽管如此，我们还是发现了APMA的自适应再平衡策略是有害的，并提出了一种新的算法，解决了它的局限性。
• 提出了一种新的批量装载算法。它特别适合流场景，其中数组的基数保持不变，并且定期分批执行具有相同插入和删除数量的更新。

RMA

RMA的目的是提供快速的面向列的扫描，同时在更新方面接近(a, b)树。

segments

段的大小是固定的，不依赖于数据结构的当前基数或容量,将段大小绑定到I/O模型的块大小O(B)，

cluster:将长序列的元素放在一起,将长序列的间隔放在一起.

在每个槽，扫描需要检查它是否为空。为了避免检查槽是否为空，我们在一个名为cards的数组中跟踪每个段的当前基数。我们把所有的元素放在片段的一端，把间隙放到另一端。奇数段将元素放在右边,偶数段将元素放在左边.

扫描对每两个片段的密集值序列执行一个紧循环。(在两个段内进行二分?)

RMAs非常像(a, b)树。实际上，组成数组的段类似于(a, b)树的叶节点。

(a, b)树在更新中有优势，而稀疏数组在扫描中有优势。

index

RMAs维护一个静态索引以改进点查找和更新。它是静态的，在RMA调整大小后构建，它包含固定数量的条目。尽管如此，单个条目还是可以改变的，在再平衡期间就会发生。索引只有分隔符键被存储，打包在一个连续的数组中。节点遍历是通过计算节点与数组中当前位置的偏移来执行的

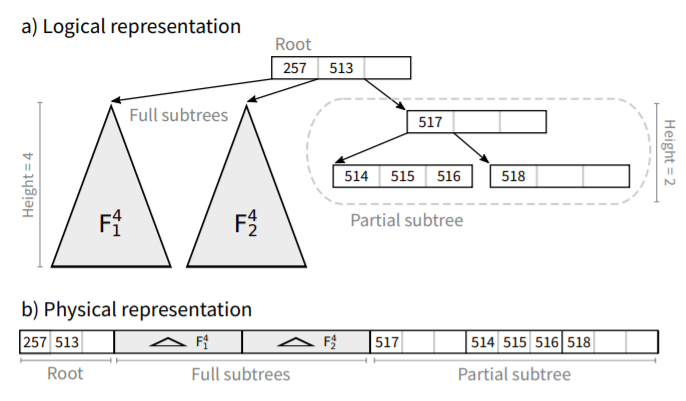
根节点包含r分隔符键，和r + 1个孩子,最左边的r个子树是高度为h - 1的满子树.槽的内容是相关段的分隔键.

re-balancing

rebalance包含两个过程,第一个过程中,将元素移动和压缩到间隔的右端或辅助附加存储中。在第二个过程中，继续前进，将元素复制到它们在数组中的最终位置。如果重新平衡的间隔小于虚拟页，我们的解决方案仍然遵循这种方案。否则，我们直接将元素从数组的页面移动并直接展开，以将parray重新平衡为一组未使用的物理页面pbuffer。最后，我们在parray和pbuffer之间一个一个地交换虚拟地址。这种技术的优点是它只对每个元素执行一次复制，而不是两次。

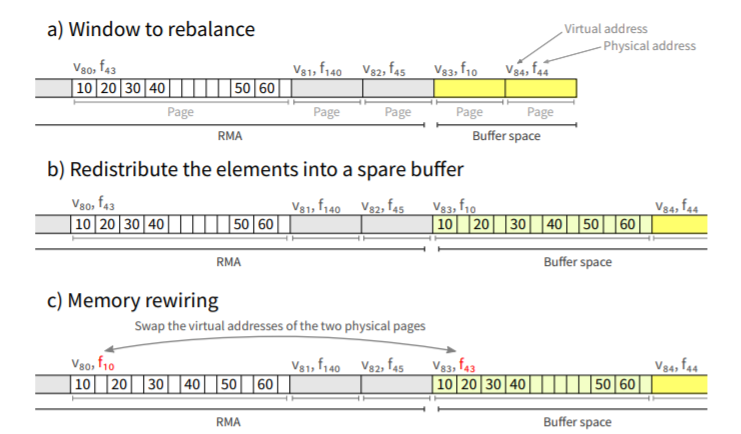
除了RMA使用的空间之外，我们还维护了一组按需分配的备用缓冲区。在重新平衡时，元素被重新分配到缓冲区空间中(参见图6b)。然后，使用内存重新连接，来自缓冲区的页面成为阵列的一部分，而阵列的旧物理页面成为备用缓冲区，以便在未来重新平衡时重用(参见图6c)。

在RMA当前使用的存储之后是备用缓冲区的物理页面(如图6a所示)。当需要扩展RMA时，我们吸收RMA中现有的备用缓冲区。如果需要缩小RMA，我们将RMA结束时释放的页面吸收到缓冲区中。好处是减轻从操作系统获取新的物理页面的开销.

bulk loading

避免在单个批处理中对相同的段进行多次再平衡。

自顶向下的策略:假设批处理中的元素已经预先排序，关键思想是从根开始遍历校准器树，然后递归地将输入序列传播给子元素。但是，如果给定节点的阈值不能满足，算法将触发再平衡，将输入序列与当前窗口中的现有元素合并。缺点是可能会造成额外的rebalance,因为顶部的阈值比较小.

自底向上的策略:首先，对插入的输入序列S进行排序。然后，该算法分三次运行。在第一次遍历中，它扫描S，只改变将插入元素的每个段的最终基数。在第二步中，它扫描被插入的片段，检查阈值是否被遵守。如果没有，它确定需要重新平衡的段间隔。最后，它对被插入的片段进行第三步。如果一个段没有标记进行再平衡，它就简单地插入来自S的相关元素,否则,rebalance第二步中的段间隔,合并相关的现有元素与排序后的序列S. 该方法可以扩展到批量插入和删除。

kv分离

改进了点查找，因为查找特定键需要遍历的内存空间更少了。

自适应 re-balancing

采用自适应再平衡来减少锤击带来的未来再平衡的数量。自适应策略被分为两个不同的部分。在第一部分中，在每次插入时，会在一个名为Detector的自定义数据结构中收集一些额外的元数据。第二部分是实际的再平衡机制，其中检查收集的元数据，以确定数组中元素的重新分布。其核心算法是递归的自适应算法。它从当前calibrator子树的顶部开始，在每一步中，它将确定分配到其子节点上的元素的数量。

detector

算法1是用于更新片段s元数据的代码，在每次插入数据之后调用。它首先在Q中记录当前操作的时间戳。时间戳可以通过某个离散的全局计数器或CPU时间戳计数器获得。此外，它还检查正在插入的键k的后继或前驱是否分别匹配kbwd或kfwd。如果两个键中有一个匹配，相关的计数器增加1，直到最大阈值SC。否则，两个计数器都减少1。当计数器达到0时，相关的kbwd和kfwd值被succk和predk替换

与kbwd关联的值3意味着，在最近的插入中，刚刚插入的键的后继至少有3次是19。因此，算法可能会猜测，未来新的插入很可能在这个范围内[predecessor(19)， 19]。

自适应算法

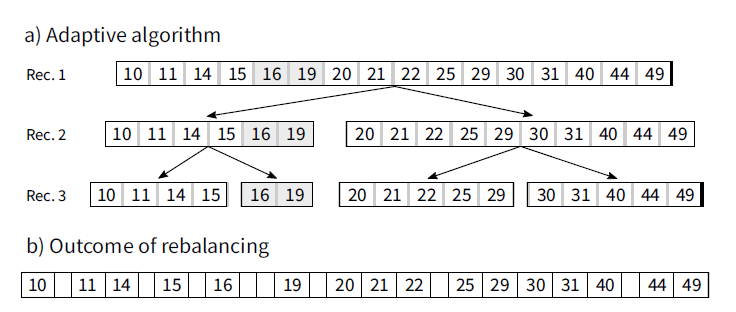
自适应算法对传统的TPMA再平衡过程进行了整合和扩充。与TPMA一样，整个过程的第一步是找到重新平衡的窗口。该操作通过遍历和验证校准树的密度阈值来完成。第二步，称为预处理阶段，包括产生一组有标记的间隔，利用检测器中的信息。如果没有创建标记间隔，则按照TPMA中的方法进行再平衡过程.否则，第三步是实际的自适应算法。该算法自顶向下遍历calibrator树，确定要放置在每个子节点上的元素数量，传输基数最小的节点中标记的间隔。这一步的输出是W中所有段的目标基数。在自适应算法的执行过程中，数组中的任何元素都不会被物理复制。只有在其结束时，当W中所有段的目标基数已经确定时，元素才会在数组中重新分布。

标记一些最近有更新的段。如果其段关联的计数器大于给定的阈值，则会发出带有kbwd或kfwd的大小为2的间隔.

自适应算法是自顶向下遍历校准器子树，根在W.

objective function 尝试将相同数量的标记间隔重新分配给每个子节点。如果不能做到这一点，例如 只有一个间隔 其余标记的间隔被移动到基数最小的子节点

在继续进行下一个递归级别之前，可能需要增加或者减少节点的目标基数。如果一个孩子v的元素密度小于其较低的阈值，那么它就会尽可能多地从其兄弟姐妹那里借用元素，从而使元素密度大于给定阈值.